TOUCH THE SECURITY Powered by Security Service G

コンピューター科学の巨人、アラン・チューリング。彼の考案した仮想のマシン=チューリングマシンはコンピューターの原理となり、その後、コンピューター実機の開発が始まる。しかし、チューリングは最初からコンピューターの原理を考案しようとしたわけではなかった。チューリングマシンからコンピューターが生まれるまでには長い物語がある。(後半)
目次
1.チューリングとカントールの論法
前半からの続き。
チューリングもカントールの論法に則り、どんな計算も可能なチューリングマシンは存在しえないこと(=数学の不完全性)を証明する。しかしチューリングは、この論法をただ模倣したのではなく、彼独自の素晴らしい"発想"を付け加える。これは、コンピューターの発展史にとって極めて重要なことだった。
何故ならば、この発想こそが後に「フォン・ノイマン型コンピューター」の特徴へと繋がるのだ。実は今、私たちが使っているコンピューター(勿論スマートフォンも)はフォン・ノイマン型である。チューリングがこの発想にたどりつかず、米国の科学者フォン・ノイマンがその意味に気づかなかったとしたら、私たちの未来は数十年は遅れていたといっても過言ではない。
そこで先ず、チューリングの証明を紐解く前に、この"発想"と現在のコンピューターとの関わりについて述べよう。これはチューリングの証明方法を理解する上でも、重要な手がかりとなる。
2.チューリングの大胆な発想とフォン・ノイマンの発見
チューリングがチューリングマシンの論文を発表した後、海の向こうの米国ペンシルバニア大学では、世界初の電子計算機「ENIAC」の開発が始まった。しかし、ENIACは、現在私たちが知っているコンピューターとはずいぶん趣が違っていて、実態は「ケーブル接続された電卓」に近いものだった。
例えば、(A+B)×Cという計算をさせたい時、足し算専用電卓と掛け算専用電卓をケーブルで接続する。足し算専用電卓にAとBという数値を入力すると、その結果がケーブルで掛け算専用電卓に送られる。掛け算専用電卓は、送られてきた数とCという数を掛け算し、結果を出力する。ENIACはそういう構造だった。そのため、現在のプログラムに相当するものはケーブル接続であり、異なる計算をさせたいときはケーブルをすべて抜いて、どのように配線したら目的の計算ができるかを考え、大量のケーブルを挿してやらなければならなかった。
このENIACの開発プロジェクトに参加した数学者フォン・ノイマンは、ケーブル方式が大いに不満だった。なぜなら、計算の設定(プログラミング)に膨大な時間がかかるし、「ケーブル接続された電卓」方式なので、複雑な計算はできないからだ。
フォン・ノイマンは、チューリングのチューリングマシンの論文を読み、落雷に打たれた。チューリングマシンの論文では、プログラムをデータと同じように扱っていたからだ。聡明なフォン・ノイマンは、この発想を応用すれば、「ケーブル接続された巨大電卓」を「電子頭脳」に進化されることができると気がついた。

By United States Army [Public domain], via Wikimedia Commons
ENIACのメイン制御パネルを2人のプログラマが操作しているところ
3.プログラムとデータを同列で扱うフォン・ノイマン型コンピューター
ENIACでもデータは真空管を使ったメモリーに保存をする。しかしプログラムは、リアルな導線の接続方法で表現する。フォン・ノイマンは、プログラムも数値に置き換えて、メモリーに置いてしまえばいいと考えた。メモリーの中のどのプログラムを実行するのかは、インディケーターを設定して「今、実行するのは○番地の命令」と示すようにすればいい。このインディケーターもデータだ。ということは、数値を自由に変えることができる。
「もし、変数Aが0より大きければ○番地のプログラムを実行。もし変数Aが0未満であれば△番地のプログラムを実行」という条件分岐や、「○番地のプログラムを実行したら、もう一度△番地のプログラムに戻る」というループができるようになる。それまでの導線を接続するプログラムと比べて、はるかに多彩で複雑な計算ができるようになったのだ。
チューリングの「プログラムとデータを同列に扱う」という発想は、彼の論文の「停止判定マシン」のところで登場する。これをフォン・ノイマンが、実用のコンピューターに応用をした。チューリングのコンピューター発展史に対する功績は、「チューリングマシンの考案」よりも「停止判定マシンの中で、フォン・ノイマン型コンピューターの原理を考案」したことの方がはるかに大きい。
4.チューリングの証明した「代数学の不完全さ」~判定停止マシン~
さて話を戻そう。果たしてチューリングは「代数学の不完全さ」をどのように証明したのだろうか。
チューリングマシンは、紙テープに書かれたデータを読み込んで、計算をする理論上の機械だった。原理的に、適切なプログラムを書いてやりさえすれば、どのような計算もできるはずだった。しかし、その万能であるはずのチューリングマシンにも計算できない実例を見つければ、「代数学は完全ではない、不完全である」ということが証明できる。
そこで、更に編み出されたものが「停止判定マシン」という理論である。
チューリングマシンのプログラム(紙テープを読み込め、ヘッドを左に移動など)は数値に置き換えることができる。ということは、紙テープに書いておくことができる(ここがフォン・ノイマンを驚愕させた)。そこでチューリングは、このプログラムを読み込んで、そのチューリングマシンが無限ループに入っていつまでも計算し続けるのか、計算を終了して停止出来るかを判定する別のチューリングマシン「停止判定マシン」を想定した(なにせ、チューリングマシンはどんな計算でもできるはずなのだ)。ここまで、チューリングの論理に穴はない。しかし、この停止判定マシンがさまざまな矛盾を引き起こし、前提である「停止判定マシンが作れる」が、否定されることになるのだ。否定されれば、万能であるはずのチューリングマシンにもできないことがあるということが証明され、ひいては「数学にもできない計算がある」ということが証明される。
チューリングは、さまざまな停止判定マシンのプログラムを、停止判定マシンに評価させるという一覧表を作った。そして、前編で紹介したカントールのロジックを使って、矛盾を指摘するのだ。
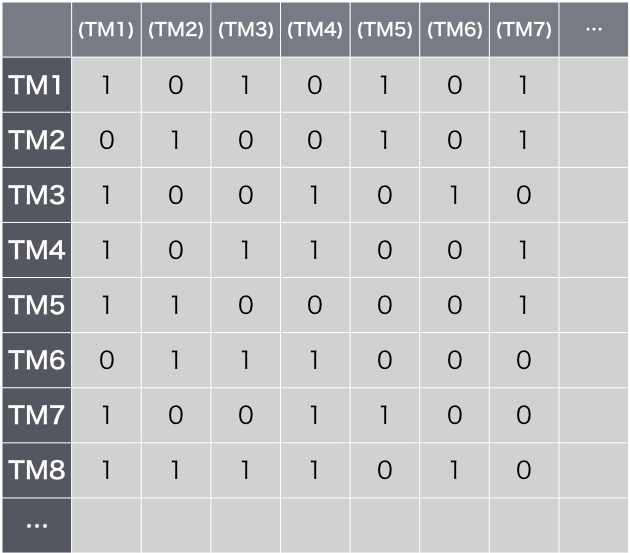
チューリングは、カントールの表とよく似た表を作った。
ここにはすべての停止判定マシンの判定結果が列挙されている。
右側と下側は無限に続く。
表のいちばん左上は、TM1という停止判定マシンが、(TM1)、(TM2)…それぞれの停止判定マシンが停止するかどうかを判定した結果だ。停止の場合は1、無限ループに入って停止しない場合は0が出力される。2行目は、TM2という別の停止判定マシンが(TM1)、(TM2)…それぞれの停止判定マシンが停止するかどうかを判定した結果になる。
ここで、対角線部分を反転させ、0010111…という新しい結果を作り出す。この0010111…は、この表の中にあるだろうか。この表には、ありとあらゆる停止判定マシンの結果が列挙されているのだから、どこかに存在しなければおかしい。しかし、存在できないのだ。1行目の結果は、1桁目が1が0に反転されているから、絶対に違う。2行目の結果は、2桁目の1が0に反転されているから絶対に違う。3桁目の結果は…と、どこまでいっても0010111…は存在できない。
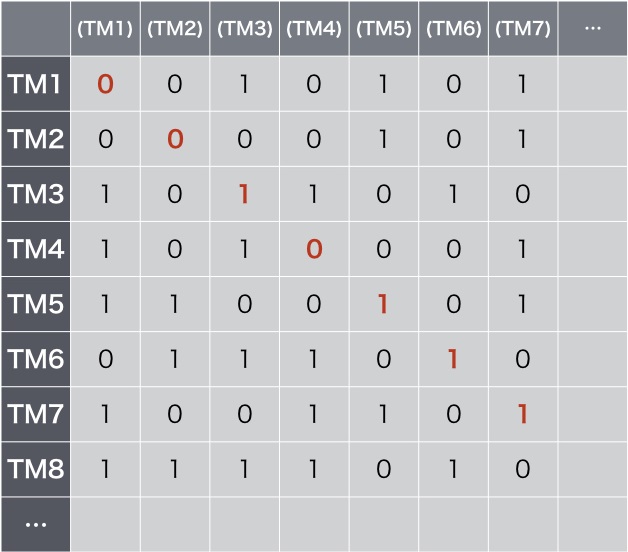
斜めを反転、新しい結果(反転)を作り出す
あらゆる結果が列挙されている表なのに、存在できない結果があるという矛盾を起こしている。これは、前提条件に誤りがあったからだ。その誤りというのは「停止判定マシンが作れる」という前提で、結論は「作れない停止判定マシンがある」ということだ。つまり、どんな計算でもできるはずのチューリングマシンにも、停止判定というできない計算が存在したということになる。
5.ハッカー的手法だったチューリングの論文
これで、チューリングは計算の不完全さを証明した。この研究を「計算の可能性と、その決定問題への応用」という論文にまとめた。タイトルだけ聞くと難しそうな論文に見えるが、ここまで辛抱強く読まれた方には、タイトルの意味がすんなりと理解できるはずだ。「計算には不可能なものがある」ということが「計算の可能性」であり、「可能か不可能かをどうやって決めたらいいのか」ということが「その決定問題」だ。
チューリングは、この論文を発表したことで、数学者として認められ、米国プリンストン研究所への留学が決まり、そこでアルバート・アインシュタインやフォン・ノイマンと出会うことになる。また、イギリス情報部もこの論文に注目をし、帰国したチューリングをヒトラー暗号の解読の仕事に抜擢することになるのだ。
チューリングの偉大さは、従来とはまったく違ったアプローチで、数学の根源的な問題に挑戦したことにある。ここでの説明を難しいと感じられている方も多いと思うが、それでも、もしこの偉業を、伝統的な数学者が伝統的な手法で行っていたとしたら、それは数学者でしか理解のできない内容になってしまうだろう。アランの手法は、多分にハッカー的な手法で、私たち門外漢にも、難しいとは言え、なんとか理解できる範囲に収まっている。
6.最後まで「自己流」を貫き通したアラン・チューリングの生涯
暗号解読の仕事を終えたチューリングは、エニグマ暗号の解読法を解説した「プロフ・ブック」と呼ばれる論文の執筆を依頼された。読むのは、暗号解読の専門家であるはずなのに、チューリングは数式を使わず、実例を多く使い、普通の人が読んでも理解できるようなものに仕上げることに心を砕いた。
しかし、チューリングは、どのような説明にすれば、普通の人にもわかりやすくなるのかよくわからず、試行錯誤をしながらの執筆だったという。それを補佐したのが、チューリングの生涯ただ一人の女性の恋人ジョーン・クラークだった。チューリングは執筆中、ジョーンを隣に座らせ、たびたび「これでわかりやすくなったかな?」とアドバイスを求めていたという。ジョーンは、チューリングの肩に頬を寄せて、執筆中の論文を覗き込み、的確なアドバイスを加えていたという。チューリングにとって、最も穏やかで幸せな時間だったに違いない。
チューリングは、ジョーンに友情とも尊敬とも恋愛ともつかない感情を抱き、結婚を約束する。自分がゲイであることも告白し、ジョーンは、二人で乗り越えることができる問題にすぎないと受け入れてくれた。二人は、1ヶ月の休暇を取り、ハイキングやサイクリングを楽しんだ。しかし、この美しく切ない恋は実らなかった。そればかりか、チューリングには悲劇的な運命が待ち受けていた。そして、感動的なエンディングを迎える。それがなにであるかは、ぜひ映画「イミテーション・ゲーム」を見ていただきたい。

イミテーション・ゲーム/エニグマと天才数学者の秘密
英政府が50年以上封印した、暗号解読の裏に隠された秘密とは?
ベネディクト・カンバーバッチが挑む、<天才数学者>の驚愕と感動の実話。
私たちは、偉人のことを偉人だと言う理由で無条件に尊敬してしまいがちだ。しかし、本来は、なぜ偉人であるかという理由を知り、それゆえに尊敬をしなければいけない。映画「イミテーション・ゲーム」は、チューリングがなぜ「コンピューター科学にとっての巨人」と呼ばれるのか、その一面を垣間見せてくれるだろう。


