フェルミ推定はくだらない？知識と経験で挑戦してみよう！

「アメリカのシカゴには何人のピアノ調律師がいるか？」といった例題で知られる“フェルミ推定“。「大手IT企業やコンサルティング会社の入社問題として出題される」、なんて噂を耳にしたことがある人も多いかもしれません。

そもそもフェルミ推定は、20世紀に活躍したノーベル物理学賞受賞者でもある物理学者、エンリコ・フェルミからその名が付けられたもの。「実際の調査が難しい課題に対し、持ちうる情報から答えを推測する方法」として、近年では「ビジネスに役立つ」「論理的思考力が鍛えられる」と注目されています。

とはいえ、フェルミ推定ってどうすればできるようになるんでしょう。シカゴにピアノ調教師が何人いるかなんて、雲をつかむような話です。それがなぜビジネスに役立つと言われているのか……？

そこで、子どもから社会人にまで数学の楽しさを伝え、1月には著書『10歳からのおもしろ！フェルミ推定』が刊行される“数学のお兄さん“こと横山明日希さんに、フェルミ推定を解くコツや、その面白さを聞きました。

フェルミ推定は「解決への道筋が決まっていない」のが面白い

――いきなりですが、フェルミ推定には「頭のいい人しか解けない難問」みたいなイメージがあるんです。シカゴにピアノの調律師が何人いるとか、どうアプローチすればいいのか見当も付かなくて……。

横山さん：いえいえ、フェルミ推定はもっと気楽に楽しめるものなんですよ！ 以前、僕が小学生の子どもたちと一緒に考えた問題だと、「僕が1年間で食べるご飯粒の数はいくつ？」というのもありましたし。

――ご飯粒！ 一気に身近になりましたね。しかもめちゃくちゃかわいい問題……。

横山さん：でしょう？ 「僕が食べる数」っていうのがいいですよね（笑）。でも、これだって立派なフェルミ推定の問題です。

横山さん：この問いだと、ご飯のお茶碗1杯がだいたい150グラム。その子は「お米30粒で1グラムぐらい」と想定していました。それなら茶碗1杯には4500粒のご飯粒がある。

じゃあ次は、「1日にご飯を何杯食べるのか？」を考えます。朝はパン、お昼は日によりけりで、夕飯はおかわりするときもあるし、2杯か3杯かなと。すると、365日なら1000杯くらい。ということは4500粒×1000杯で、「君は1年間にご飯粒を450万粒も食べてるね！」と計算するわけです。

――すごい！ あっという間に答えが出ましたね……！

横山さん：フェルミ推定の基本的な考え方は、「集めた情報を組み合わせて、もっともらしい数を算出する」というものです。“推定“ですから、出てくる数はあくまで概算。答えが合っているかどうかより、「未知の疑問に対して、どんな素材があれば解決するか？」を考えるものだと思っています。 数字の設定次第で正しい結果からは少しずれてしまう場合もありますが、多少のズレは特に気にせずで大丈夫ですよ。

その「素材」も、決まった正解があるわけではないのがフェルミ推定の面白いところ。解決への道筋は、いくつもあるんですよ。

――どういうことでしょう？ なにか例題はありますか？

横山さん：そうですね……。講座で「日本中の電車の線路を全て合わせると、何キロメートルになる？」という問題をやったことがあります。まず思いついたのは「日本に駅はどれくらいあるか推定して、それに駅間の距離を掛け算する」というアプローチでした。

でもその講座には鉄道に詳しい人がいて、「JR九州の営業キロは約2000キロメートル」って知っていたんです。それがわかるなら、九州の面積と日本の面積を比較して類推することもできる。2つの方法で計算してみたら、結果がほぼ同じになったんですよ。このときはテンション上がりましたよ。

――なるほど。ひとつの問題でも、いろんな解き方があるわけですね。

横山さん：「人間の頭に生えている髪の毛は何本あるか？」という問題のときも、「頭を半球と考えて表面積を算出し、1平方センチメートルあたりの本数をかける」とか「髪の毛の1本の太さとポニーテールの直径を比較する」とか、いろんなやり方で解こうとする人がいました。「髪の毛を全部剃って重さを計って、1本あたりの重さと比べる」という案もありましたよ。

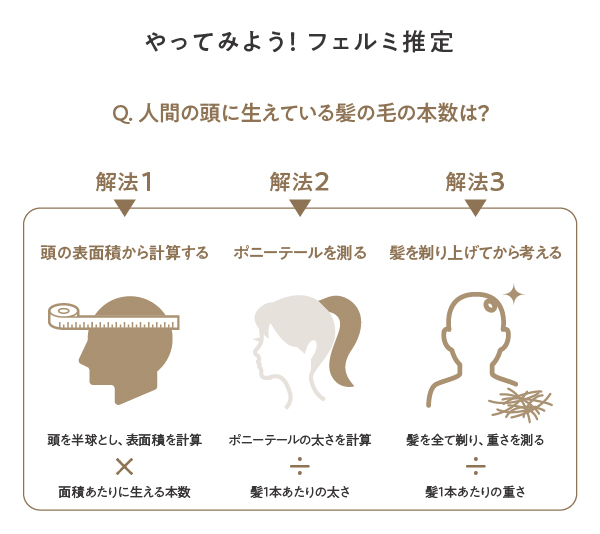
――アイデアを聞くだけですごく面白いですね！

横山さん：フェルミ推定には「他のやり方もあるのでは？」と、発想力を鍛える側面もあります。そのうえで、「既に知っている数字」や「調べればわかる数字」を、いかに組み合わせるかが答にたどり着くポイントになります。

求めている答えに対して、どのような要素が必要なのか、その要素をどう扱えば答えにたどり着けるのか……。そうしたプロセスが、ビジネス的な視点で注目されているのだと思います。

入社試験でフェルミ推定をさせる企業は、なにを見ているのか？

――なんだか自分でもフェルミ推定が解ける気がしてきました。解くためのコツみたいなものはありますか？

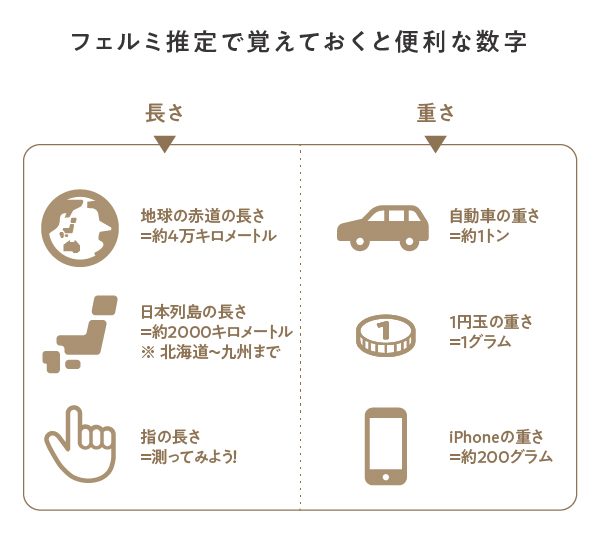
横山さん：単位ごとに基準となる数をいくつか覚えておくといいと思います。長さなら、「地球一周分の赤道の長さ」や「日本列島の縦の長さ」といった長いもの、「鉛筆1本の長さ」や「自分の指の長さ」といった短いものを覚えておく。重さなら、車がだいたい1トン、iPhoneが200グラム、1円玉が1グラムという感じですね。

――知らない数でも、なにか基準があれば「これよりは大きい」「これよりは小さい」と類推できますね。

横山さん：その通りです。ビジネス関連なら、日本にある企業の数が約420万社とか、コンビニ1日の売上がだいたい50万円くらい、とかが役立つと思います。

▲他には、「日本の総人口（1.2億人）」「日本の世帯数（5000万世帯）」「15歳未満の人口（約1500万人）」などは知っておくと便利かも

――しかし、それって裏を返せば、知識がないと解けないということでしょうか……？

横山さん：そんなことはありませんよ。フェルミ推定に必要なのは「知識」と「経験」なんです。知識がないなら、自分の経験から導けばいい。

さっきの「日本列島の長さ」を考えてみましょうか。僕は茨城県出身なので、「地元から東京まで、電車で行くとだいたい2時間半くらい」というのは知ってるんですよね。

電車の平均時速が60キロメートルだとすると、茨城から東京までの距離は150キロメートルくらい。東京から同じくらい離れている西の地方となると静岡かな、名古屋まではその倍くらいかな、ということは東京・名古屋間は300キロメートルくらいで、そうなると本州の長さは……類推していけるわけです。

――今の例だと、日本地理の「知識」と、茨城から電車で上京した「経験」を組み合わせているわけですね。

横山さん：未知の課題に直面したとき、経験から「あのときのアレだ！」と引き出せる人はやっぱり強いですよね。日ごろからアンテナを立てているから、経験を知識に変えることができるわけで。

もちろん、既知の知識から類推したり、さらに必要な知識を調べたりできる人も強い。フェルミ推定がよく入社試験で使われるのも、こうした「未知の課題に対するアプローチ」を確かめるのに適しているからだと思います。

問題に答えを出せるかだけでなく、その人がどういう知識を持っているのか、どういう経験をしてきたのか、どういう道筋を経て答を導いたのか、それを分かりやすく説明できるのか……と、フェルミ推定を解くだけでさまざまな特性が見えてきますから。

――知識、経験、プレゼン能力まで短時間で見抜ける……。なるほど、入社試験に使われるわけですね。工数の見積もりとか、人によってはそれとは知らずに日常的にフェルミ推定っぽいことをやっているケースも多そうです。

横山さん：ただ僕としては、もっとゲーム感覚でフェルミ推定を楽しんでもらいたいんです。

確かにフェルミ推定はビジネスにも役立ちますし、僕も講座で「全体像をつかめる」「経営視点が身につく」という話はしています。でもフェルミ推定の面白さはそれだけに留まりませんし、数学が苦手な人にも興味を持ってもらえるようにイメージを変えたいんですよね。

――では、ビギナーでもチェレンジできそうな問題をいくつかお聞きできますか？

横山さん：「鉛筆1本で何メートルの線が書けるか？」とかどうですか？

――むむ……。実際に鉛筆で50cmくらい線を引いて、芯が何ミリ減ったかを計れば計算できそう……。

横山さん：いいですね。まずはプロセスを考えてみるのが大事ですから。他にも講座で参加者さんと一緒に考えたお題だと「自分が1年間で見ているYouTube広告の再生時間は？」「日本で1日に消費される割り箸は何本？」「人は1時間の会議で何文字ぶんしゃべる？」とかありますよ。

ちょっと個性的なものだと「日本でプレイされた『スーパーマリオブラザーズ』で、マリオは累計何回死んでいる？」なんていうのもありました。さすがにこれは難しいかもしれないので（笑）、「直接答えにつながらない情報であれば、◯つまでは調べてもOK」というルールを加えて遊んでみるのもいいかもしれませんね。

▲上記は「スクリーンタイム＝“広告を含まない”動画の総再生時間」として扱っているため、実際の累計再生時間はもう少し短くなる。1年で約1日分という数字を「そんなに!?」と思うか、「あれ、意外と……」と思うかはあなた次第

▲例題をざっくり概算してみるとこんな感じ。「マリオ」の例は、「ミス回数増加のパラメータをどう設定するか」はもちろん、周回プレイするケースや途中で止めてしまった人、移植版のプレイヤーは考慮できていないので、まだまだ精度を上げる余地はある

「フェルミ推定は間違えていいし、この世界は間違えていい」

――横山さんは子ども向けの算数講座も開いていますよね。子ども向け講座だからこそ、意識されていることはありますか？

横山さん：「楽しい」と思ってもらえることですね。それこそゲーム感覚で、算数にわくわくする時間を少しでも提供できればいいなと思っています。

算数に限らず、勉強って「先生が正解というものが正解」と思ってしまうじゃないですか。でもフェルミ推定は、さまざまなプロセスを楽しむもので、答えもアバウト。そもそも問題を出している僕も正解がわからない（笑）。だから「僕もわかんない」「どんどん間違えていいから」と伝えて、発言するハードルを下げるように心がけています。

――子ども向け講座では、どんな例題を出しているんですか？

横山さん：子どもはある程度答えが決まっていたほうが考えやすいので、「この国語辞典は何ページあるでしょう？」みたいな問題が多いですね。

実際に「国語辞典ってこんな感じだよね〜」と実物を見せてあげると、「ア行のページ数を教えて」とか「1ページに何個の単語があるんですか」とか、たくさん質問が飛んできますよ。「国語辞典に指を当ててみてください」って、指の長さから辞典の厚みを推定しようとする子とかも（笑）

横山さん：一度「間違えてもいい」という場面を設定すると、子どもたちはちゃんと理解して実践してくれると感じますね。

――子どもたちは……ということは、大人たちは？

横山さん：大人たちのほうが数学に抵抗感を抱いているんですよね……。答えを導くプロセスまではわかっても、実際に計算するところで手が止まってしまうんです。「計算して答を出す」という行動にためらいがあるのかもしれません。

――「間違えてはいけない」「間違えたら恥ずかしい」と思ってしまうんでしょうか……？

横山さん：そうみたいですね。言い換えれば、普段から失敗が許されない世界で戦っているということだと思いますが……。でも、むしろビジネスの世界のフェルミ推定は「間違えてからがスタート」だと思うんですよ。

ビジネスでフェルミ推定を使うのは、新規事業の工数を見積もったり、売上げを予想したりするみたいな、計画のかなり初期段階にあたると思うんです。その後、プロジェクトを動かせば、これまで見えていなかった実態が見えてきます。そうなれば、実態に合わせて計画を見直しますよね。

――最初の計画段階で、数がぴったり合っているほうが珍しいですもんね。

横山さん：そうです。大切なのは計算結果ではなく、計算式（プロセス）のほう。「この数字が間違えていた」「もっとこういう数字が必要だ」と、計算式の精度をブラッシュアップしてもいいわけです。さらに「この数字を変えれば、この数字があがる」といった裏づけがあれば、計画も見直しやすくなります。

――それなら、そもそも最初から計算式を間違えている可能性も…？

横山さん：もちろん、十分に考えられるでしょうね。だからこそ、いかにさまざまなプロセスを思いつけるか、他の計算式を作れるかが大事になってきます。

▲横山さんの著書『10歳からのおもしろ！フェルミ推定』。本では、「プールにタピオカミルクティーMサイズは何杯入る？」や「1冊のノートに、好きなコの名前は何個書ける？」等の問題が紹介されている

――そこでフェルミ推定の考え方が生きてくるわけですね。答えに至るプロセスは、ひとつじゃない。

横山さん：そうなんです。だからもっと、気軽にフェルミ推定に取り組んでみてほしいですね。フェルミ推定は間違えてもいいし、この世界自体、間違えても大丈夫なことは皆が思っている以上にたくさんあるんです。

学生時代にテストで評価されてきた記憶から、多くの人が「数学＝間違えてはいけないもの」というイメージを持っていると思います。それってすごくもったいない。学校の「外」にある数学の世界は、もっと自由で楽しいものなんですよ。

意外な結果に「こんなにたくさん!?」とびっくりする、その楽しさを大人も子どもも感じてもらえたらいいですね。フェルミ推定をきっかけに、答えのない問いを考える楽しさが伝わればと思います。

文＝井上マサキ／図版とイラスト＝藤田倫央／編集＝伊藤 駿（ノオト）